Inkrementalgeber
Encoder für präzise Positions- und Drehzahlerfassung
Ratgeber Inkrementalgeber
Inhalt
Was ist ein Inkrementalgeber?
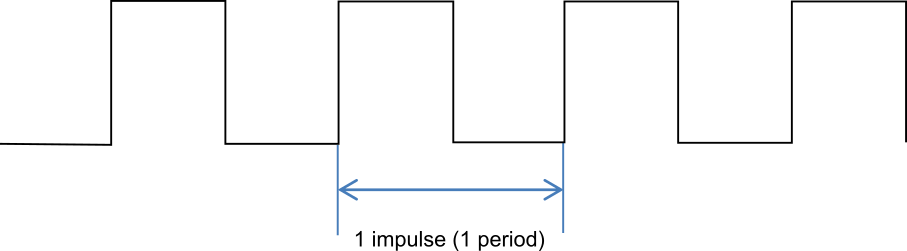
Inkrementalgeber sind Drehgeber, die ihr Ausgangssignal in Form von Impulsen ausgeben. Ein Impuls entspricht einer Periode, dem Inkrement. Daraus leitet sich auch der Name dieses Drehgebertyps ab. Aufgrund ihrer Eigenschaft, Drehbewegungen zu erfassen, und der Form ihres Signals werden Inkrementalgeber auch als Drehimpulsgeber bezeichnet. Das Messprinzip mit Impulsen unterscheidet sich grundlegend von z. B. Potentiometern und Absolutwertgebern.
Die Anzahl der Impulse, die pro volle Umdrehung der Welle am Ausgang erzeugt werden (Impulse pro Umdrehung, Imp./Udr.), ist die wichtigste Kenngröße zur Bestimmung der Winkelgenauigkeit eines Inkrementalgebers. Dieser Wert ist in jedem Datenblatt eines Inkrementalgebers angegeben.
Zur Auswertung der Signale von Inkrementalgebern ist immer eine externe Auswerteeinheit, z. B. ein Zähler, erforderlich.
- Soll der Winkel erfasst werden, müssen die Informationen aus den Inkrementen ausgewertet werden. Liefert der Inkrementalgeber z. B. 360 Impulse/Umdrehung, so entspricht 1° genau einem Impuls.
- Für die Messung der Winkelgeschwindigkeit (Winkeländerung pro Zeiteinheit) wird die Anzahl der Impulse pro Zeiteinheit berechnet.
Generell sind bei der Signalauswertung einige Punkte zu beachten, siehe Signalauswertung von Inkrementalsignalen.
Funktionsprinzipien
Für die technische Realisierung eines Inkrementalgebers stehen verschiedene Sensorprinzipien zur Verfügung. Die wohl am weitesten verbreitete Technologie ist die optoelektronische Abtastung, die bei optischen Drehgebern zum Einsatz kommt. Eine weitere Möglichkeit stellen magnetische Messprinzipien dar. Auch „Hall-Encoder“ mit inkrementalen Ausgängen werden angeboten. MEGATRON setzt hier ausschließlich auf moderne, gradientenbasierte Hallsensoren.
Optische vs. magnetische Inkrementalgeber - ein kurzer Vergleich
Optische Inkrementalgeber liefern besonders genaue Signale und eignen sich für Anwendungen, die eine hohe Auflösung erfordern. Sie sind jedoch empfindlicher gegenüber Staub und Feuchtigkeit, was sie in rauen Umgebungen anfälliger macht. Magnetische Inkrementalgeber sind robuster gegenüber Umwelteinflüssen wie Schmutz und Feuchtigkeit und daher besser für den Einsatz in rauen Industrieumgebungen geeignet, bieten aber im Allgemeinen eine geringere Auflösung.
Optische Inkrementalgeber
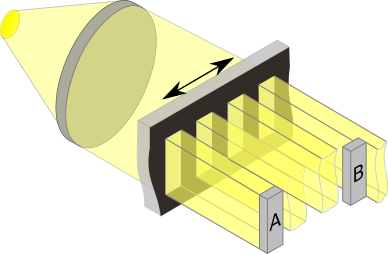
Die schematische Darstellung zeigt stark vereinfacht das abbildende Messprinzip eines optischen Encoders. Die beiden Detektoren A und B werden während der Drehung des Kodierrades (schwarz) räumlich versetzt beleuchtet, wodurch Impulse erzeugt werden.
Die optische Sensorik bietet eine Reihe von Vorteilen, die optische Drehgeber zu den wichtigsten Inkrementalgebern machen. An erster Stelle ist hier die Tatsache zu nennen, dass das Messverfahren der integrierten Sensorelemente selbst Inkremente erzeugt. Eine Übersicht über optische Drehgeber finden Sie hier.
Das optische System eines modernen inkrementalen Drehgebers besteht mindestens aus
- einer Licht emittierenden Diode (LED)
- einem Kollimator, der das LED-Licht parallel ausrichtet
- einem Kodierrad, mit abwechselnd durchlässigen und undurchlässigen (oder reflexive und absorbierende) Bereiche
- dem Fotodetektor, der das einfallende Licht der LED erfasst und in ein elektrisches Signal umwandelt
Zwei Verfahren haben sich auf dem Markt etabliert: Das transmissive (bildgebende) und das reflektive (interferentielle) Verfahren. Beim transmissiven Verfahren wird das Kodierrad durchleuchtet, während beim reflektiven Verfahren der Lichtstrahl von der Oberfläche des Kodierrades zurückgeworfen (reflektiert) wird und Interferenzeffekte ausgenutzt werden.
Kurze Erläuterung des Übertragungsverfahrens:
Das Licht wird kollimiert (parallelisiert) und durchläuft das Kodierrad. Das Rad sorgt dafür, dass periodisch abwechselnd helle und dunkle Bereiche auf die Detektoren treffen. Die Signale der beiden Photodetektoren sind in der Regel um 90° phasenverschoben. Aus der Abfolge der Signale bzw. ihrem Abstand im Ausgangssignal kann die Drehrichtung ermittelt werden.
Der Aufbau variiert je nach Anforderung. Zusätzliche Elemente im Aufbau des Sensors erzeugen z.B. einen Referenzimpuls, der nur einmal pro Umdrehung ein Signal auf einem dritten Kanal erzeugt. Mit dieser Referenz kann der absolute Winkel berechnet werden. Das bedeutet, dass die Anzahl der Impulse von der Referenz aus gezählt wird. Geht der Zählerwert durch eine Unterbrechung der Spannungsversorgung verloren, kann die Information über den Absolutwinkel durch eine Referenzfahrt wiederhergestellt werden.
Kodierräder für optische Encoder
Kodierräder werden aus verschiedenen Materialien hergestellt, in der Regel aus Metall, Glas oder Kunststoff. Für preisgünstige Kodierräder wird überwiegend Kunststoff verwendet. Kodierräder aus Metall sind sehr robust. Vergleicht man Metall mit Glas oder Kunststoff, so lassen sich bei gleichem Durchmesser mit Metall im transmissiven Verfahren nicht so hohe optische Auflösungen erzielen. Beim reflektiven Verfahren wird die Inkrementalstruktur auf das Kodierrad aufgedruckt und es können feinere Strukturen realisiert werden.
Halleffekt-Inkrementalgeber
Hall-Effekt-Drehgeber sind auch mit inkrementalen Ausgängen erhältlich. Die Messtechnik ist wie bei den optischen Drehgebern berührungslos und daher (abgesehen von der Lagerung) nahezu verschleißfrei. Die Vorteile der Halleffekt-Inkrementalgeber liegen vor allem in der praktisch unbegrenzten Lebensdauer der Sensorik (keine Alterung der Leuchtdioden) und der hervorragenden Schockfestigkeit. Nachteilig können die Empfindlichkeit gegenüber externen Störfeldern und die etwas verzögerte Signalübertragung (Updaterate) sein. Zur Erläuterung des Messprinzips von Hall-Effekt-Drehgebern siehe daher Ratgeber Absolutwertgeber. Für eine genauere Analyse der Vor- und Nachteile der verschiedenen Drehgeber-Technologien siehe Ratgeber Drehgeber.
Genauigkeit und Auflösung unter verschiedenen Bedingungen
Die Genauigkeit eines Inkrementalgebers wird durch mehrere Faktoren beeinflusst:
- Auflösung des Gebers: Die Anzahl der Pulse pro Umdrehung bestimmt zum großen Teil die Messgenauigkeit. Denn ein Geber kann eine hohe Auflösung haben, aber durch äußere Einflüsse oder Materialtoleranzen an Genauigkeit einbüßen.
- Signalqualität: Die Qualität des Ausgangssignals kann von Rauschen oder Signalverzerrungen beeinträchtigt werden.
- Betriebsbedingungen: Schmutz, Staub, Feuchtigkeit oder extreme Temperaturen können die Genauigkeit, besonders bei optischen Gebern, reduzieren.
- Montage und Ausrichtung: Eine exakte Installation minimiert Abweichungen.
- Mechanische Belastung: Vibrationen oder mechanische Spannungen können die Genauigkeit ebenfalls beeinflussen.
Signalauswertung von Inkrementalsignalen
Kanäle, Auflösung und Drehsinn
Inkrementalgeber haben in der Regel mehrere Signalausgänge. Gibt ein Inkrementalgeber mehrere Signalpakete aus, so wird in diesem Zusammenhang der Begriff "Kanal" verwendet. Zum Beispiel „Kanal A“ und „Kanal B“. In der Literatur wird anstelle des Begriffs „Kanal“ auch der Begriff „Spur“ oder im Englischen „Track“ verwendet.
Beispiel:
Ist im Datenblatt eines inkrementalen Drehgebers der Wert 360 Imp./Udr. angegeben und besitzt der Drehgeber die elektrischen Signalausgänge „A“ und „B“ (“Kanal A“ und „Kanal B“), so werden am Ausgang „A“ 360 Impulse pro Wellenumdrehung (pro 360°) und ebenfalls am Ausgang „B“ weitere 360 Imp./Udr. 90° vor- oder nacheilend zu den Impulsen des Kanals A ausgegeben. Insgesamt erzeugt der Geber also für die beiden Kanäle A und B 720 Imp./Udr. pro volle Wellenumdrehung (360°).
Die Anzahl der Impulse pro Umdrehung (Imp./Udr.) wird auch als Auflösung bezeichnet. Je höher dieser Wert (Imp./Udr.) ist, desto höher ist die Winkelauflösung des Drehgebers.
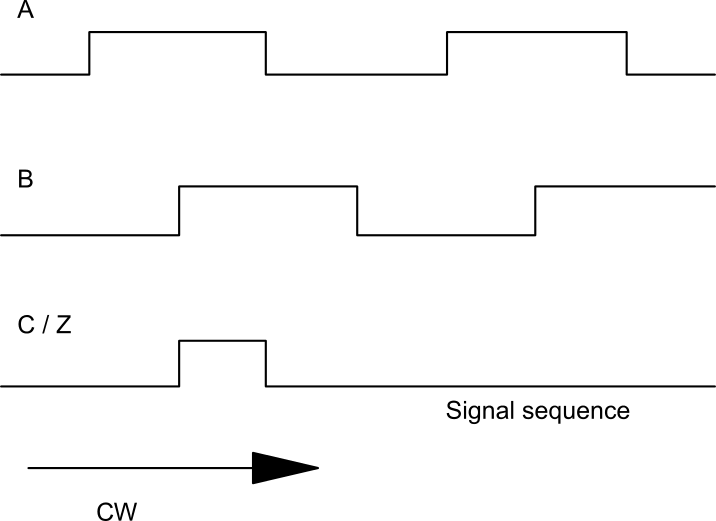
Die Rechtecksignale von „Kanal B“ sind den Signalen von „Kanal A“ entweder um 90° voraus oder um 90° nacheilend. Ob das Signal von „Kanal B“ dem Signal von „Kanal A“ um 90° vorauseilt oder nacheilt, hängt vom Produkt ab und ist im Datenblatt angegeben. In der Regel findet sich dort eine Abbildung der Signalausgangsfunktion in Verbindung mit der Angabe dem Drehsinn, in der die Signalfolge der Kanäle dargestellt ist.
Beispiel: In der nebenstehenden Abbildung ist als Drehsinn als CW (CW=ClockWise) definiert.
Betrachtet man den Encoder von vorne (das Wellenende des Winkelcodierers zeigt in Richtung des Betrachters) und dreht die Welle des Encoders im Uhrzeigersinn, so eilt das Signal von „Kanal B“ dem Signal von „Kanal A“ um 90° hinterher. Dreht sich die Welle dagegen gegen den Uhrzeigersinn, so eilt das Signal von „Kanal B“ dem Signal von „Kanal A“ um 90° voraus.
Dieser Zusammenhang kann in einer Auswerteeinheit zur Drehrichtungserkennung genutzt werden. Impulszahl, Impulslänge und Periodendauer von Spur A und Spur B sind identisch. Beim Austausch eines Drehgebers durch einen anderen Typ sind diese Eigenschaften entscheidend, da die Programmierung der Auswerteeinheit nicht geändert werden muss, wenn die Signalfolgen der auszutauschenden Produkte identisch sind.
Z-Spur / Index Signal
Häufig ist optional eine weitere Spur wählbar, die sogenannte Indexspur oder „Z-Spur“. Am Ausgang der Z-Spur wird bei jeder vollen Wellenumdrehung (360°) ein Indexsignal in Form eines einzelnen Rechteckimpulses ausgegeben.
Das Indexsignal hat zwei Hauptfunktionen:
- Als Nullpunktreferenz: Nach einer Spannungsfreiheit kann mit Hilfe des Indeximpulses ein definierter Nullpunkt angefahren werden.
- Als Referenzimpuls: Insbesondere bei Drehgebern, die mit sehr hohen Betätigungsgeschwindigkeiten betrieben werden, hat der Referenzimpuls als separater Zählimpuls für eine volle Betätigung / Umdrehung eine Kontrollfunktion.
Fallbeispiel:
Es wird geprüft, ob zwischen zwei aufeinander folgenden Indeximpulsen die Anzahl der „normal“ gezählten Impulse mit der erwarteten Anzahl übereinstimmt. Wird z. B. ein Winkelcodierer mit der Spezifikation 16000 Imp./Udr. verwendet und die Auswerteeinheit zählt weniger als 16000 Impulse pro volle Umdrehung, so liegt ein Fehler vor.
Flankenauswertung / Quadratursignal
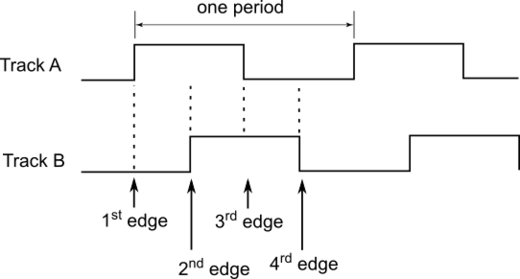
Vorteilhaft ist der Signalversatz von 90° zwischen den Rechtecksignalen der Kanäle A und B. Ein Rechtecksignal hat pro Spur und Signalperiode eine steigende und eine fallende Signalflanke.
Die Flankenfolge für die Spuren A und B einer Signalperiode ist wie folgt
Spur A steigende Flanke (1) → nach einer ¼ Periode Spur B steigende Flanke (2) → nach einer ½ Periode Spur A fallende Flanke (3) → nach einer ¾ Periode Spur B fallende Flanke (4).
Wird in einer Auswerteeinheit nicht nur die steigende Flanke einer Spur, sondern die steigende und die fallende Flanke beider Spuren A und B ausgewertet, so kann mit diesem Verfahren die Anzahl der Impulse vervierfacht werden. Dies entspricht einer Erhöhung der Genauigkeit um den Faktor 4, ohne dass konstruktive Änderungen am Geber vorgenommen werden müssen.
Beispiel:
Ist im Datenblatt des Inkrementalgebers eine Auflösung von 1024 Imp./Udr. angegeben, so würde diese bei Flankenauswertung vervierfacht, was 4096 Signalen pro Umdrehung pro Kanal entspricht. Die soeben beschriebene Flankenauswertung wird auch als „Quadratursignal mit Richtungsinformation“ bezeichnet. Eine Flankenauswertung kann z.B. auf Basis des von MEGATRON angebotenen integrierten Schaltkreises LS7083 realisiert werden.
Maximale Geschwindigkeit und Grenzfrequenz
Inkrementalgeber können nicht mit beliebig hoher Geschwindigkeit betrieben werden. Es gibt mechanische und/oder elektronische Limitierungen:
Die mechanischen Limitierungen können dem Datenblatt entnommen werden und haben folgende Ursachen:
- Max. Geschwindigkeit des Wellenlagers (gilt nur für Encoder mit eigenem Wellenlager, siehe Shaft Encoder). Hier befindet sich die maximal zulässige Betätigungsgeschwindigkeit oft unter 10000 Udr./min.
- Der Exzentrizität (Unwucht) der Mechanik. Bei optischen Encodern wird diese insbesondere durch die Unwucht des Kodierrades verursacht. Die maximale Betätigungsgeschwindigkeit kann hier aber durchaus bis zu 60.000 Udr./min. betragen. Bei magnetischen Kit-Encodern gibt es diese Begrenzung in der Regel nicht.
Die elektronische Limitierung lässt sich berechnen. Das Ergebnis der Berechnung ist die „theoretisch maximal mögliche Betätigungsgeschwindigkeit“.
- Dies liegt an der Grenzfrequenz der Elektronik. Eine höhere Frequenz als die Grenzfrequenz kann von der Elektronik nicht verarbeitet werden. Je höher die Grenzfrequenz und je niedriger die Auflösung des Gebers, desto höher ist die theoretisch mögliche Betätigungsgeschwindigkeit. Mit der folgenden Formel kann aus der Grenzfrequenz die theoretisch maximale Betätigungsgeschwindigkeit berechnet werden:
\(max. rpm =\frac{\text {cut-off frequency} \frac {1} {s} * 60 }{ \text {number of pulses}}\)

Nachstehend sind zwei Beispiele für die Berechnung der theoretischen maximalen Betätigungsgeschwindigkeit aufgeführt.
Beispiel 1:
Gewünscht ist eine Auflösung von 512 Imp./Udr. Die Grenzfrequenz des Encoders ist mit 100 kHz angegeben. Man erhält
\({100000 \cdot 1/s\cdot 60 \text{ s} \over 512} = 11718 \text { rpm} \)
Ergebnis: Die theoretische, maximal zulässige Betätigungsgeschwindigkeit ist 11718 Udr./min.
Beispiel 2:
Gewünscht ist eine Auflösung von 10000 Imp./Udr. Die Grenzfrequenz des Encoders ist mit 100 kHz angegeben. Ergebnis: Die theoretische, maximale Betätigungsgeschwindigkeit beträgt 600 Udr./min.
\({100000 \cdot 1/s \cdot 60 \text{ s} \over 10000} = 600 \text { rpm} \)
Ein Vergleich zwischen der maximalen theoretischen und der mechanisch zulässigen Betätigungsgeschwindigkeit zeigt, welche für die Anwendung relevant ist: Der niedrigere der beiden Werte ist relevant!
Toleranzen und Abweichungen optischer Inkrementalgeber
Kein Inkrementalgeber liefert perfekte Signale. Für optische inkrementale Drehgeber wird nachfolgend beschrieben, welche Unsicherheiten bzw. Toleranzen für die Signale dieser Drehgeber zu berücksichtigen sind. Das optische System besteht aus dem Geberrad selbst und dem Gebermodul bzw. der Baugruppe, die die LED und den Fotodetektor enthält. Alle Elemente erzeugen im Zusammenspiel eine gewisse Abweichung von der idealen rechteckigen Signalform und der idealen Flankenlage. Diese Toleranzbeziehungen werden im Datenblatt eines optischen inkrementalen Drehgebers beschrieben und helfen dem Anwender bei der genaueren Analyse der Messdaten.
Die Darstellung erfolgt in der Regel durch eine Abbildung der Signale der Kanäle A, B und ggf. Z. Anhand der nebenstehenden Abbildung werden die Zusammenhänge an Beispielen erläutert.
Die Symbole haben die folgende Bedeutung:
C entspricht einer Signalperiode
P steht für einer ½ Signalperiode
S für ¼ Signalperiode
Ф ist der Phasenbezug zwischen den Kanälen A und B
Im Idealfall gilt also C = 2 * P = 4 * S = S1 + S2 + S3 + S4.
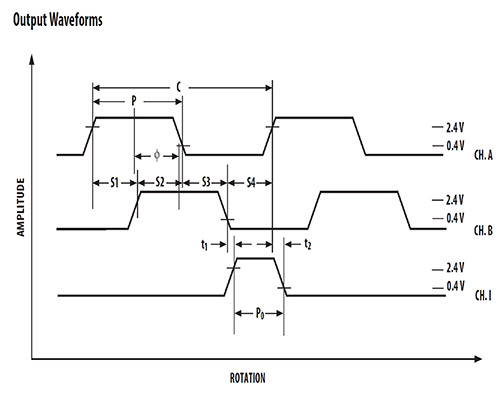
Beispiel für die Beschreibung des Toleranzfeldes einer viertel Periodendauer
Im Idealfall besteht ein Inkrement und damit eine Periode aus vier äquidistanten Signalanteilen (C/4). Da in der Praxis eine Signalperiode nicht aus vier gleichen Teilen besteht, wird das mögliche Verhältnis und damit das Toleranzband der vier Teile einer Signalperiode (T) zueinander beschrieben. Der folgende Term besagt, dass ein Viertel der Signalperiode um ein Zwölftel der Signalperiode schwanken kann:
\(S1,S2,S3,S4 = \frac {C} {4} \pm \frac {C} {12}\)
Beispiel für die Beschreibung des Toleranzfeldes einer halben Periodendauer
Ein Inkrement und damit eine Signalperiode besteht im Idealfall aus zwei äquidistanten Signalanteilen (C/2). Da eine Signalperiode nicht immer genau aus zwei gleich langen Wellenpaaren besteht, wird das mögliche Verhältnis der beiden Wellenpaare einer Signalperiode (T) zueinander beschrieben. Der folgende Term besagt, dass eine halbe Periodendauer bzw. eine halbe Signalperiode bzw. eine halbe Wellenlänge um plus/minus ein Zwölftel vom Ideal abweichen kann.
\(P = \frac {C} {2} \pm \frac {C} {12}\)
Beschreibung des möglichen Phasenversatzes zwischen Kanal A und B
Im Idealfall beträgt die Phasenverschiebung zwischen den Kanälen A und B genau 90° (neunzig Grad). Diese 90° werden durch das Verhältnis C/4 dargestellt. Ein Viertel einer Signalperiode entspricht also 90°. Der Fehler kann in diesem Fall ± C/24 betragen, also plus/minus ein Vierundzwanzigstel. Ein Vierundzwanzigstel entspricht 360°/24, was einem möglichen Phasenfehler von plus/minus 15° entspricht. Die Inkrementbeziehung zwischen den Kanälen A und B kann also im Bereich von 90° ±15° und die Phasenbeziehung zwischen den Kanälen A und B im Bereich von 75°...105° liegen.
\(Ф = \frac {C} {4} \pm \frac {C} {24}\)
Beschreibung des Toleranzbandes der Pulslänge des Index-Impulses (Kanal Z)
Der Indeximpuls wird bei kontinuierlichem Betrieb der Welle in einer Richtung einmal pro 360° ausgegeben. Eine Periode entspricht C. Die Darstellung C/4 bedeutet, dass der Indeximpuls im Idealfall ¼ der Länge einer Signalperiode entspricht. Die Pulsbreite des Indeximpulses kann vom Ideal, d.h. der Länge einer viertel Signalperiode (=C/4), um plus/minus ein Zwölftel einer Signalperiode abweichen.
Das bedeutet, dass die Pulsbreite des Indeximpulses zwischen 1/3 (=C/3) und 1/6 (=C/6) einer Signalperiode variieren kann.
\(Po = \frac {C} {4} \pm \frac {C} {12}\)
Sinus-Cosinus-Interpolation
Je mehr Impulse pro Umdrehung bei einem optischen Drehgeber realisiert werden, desto kleiner wird die Strichbreite der Inkremente auf dem Geberrad. Das optische System eines Winkelkodierers ist jedoch nur in der Lage, Inkremente bis zu einer bestimmten Strichbreite zu erfassen. Beispielsweise können auf einem Kodierrad mit 10 mm Durchmesser aufgrund der geringen Baugröße keine 10000 Striche aufgebracht werden. Sollen Inkrementalgeber mit kleinem Gehäusedurchmesser und hoher Auflösung realisiert werden, so erfolgt dies häufig auf der Basis einer Sinus-Cosinus-Interpolation.
Bei diesem Verfahren wird das optische System des Drehgebers nicht wie bei einem konventionellen optischen Inkrementalgeber so genutzt, dass abrupte Zustandswechsel zwischen Transmission und Transmissionsunterbrechung bzw. Reflexion und Reflexionsunterbrechung auftreten. Stattdessen wird ein möglichst fließender Übergang zwischen keiner und maximaler Transmission bzw. Reflexion realisiert. Dieser fließende Übergang führt zu einem sinusförmigen Signalverlauf. Um einen zweiten Kanal zu realisieren, der ein Kosinussignal erzeugt, werden eine weitere LED und ein Fototransistor benötigt. Das Sinus- und Kosinussignal werden anschließend digitalisiert. Hierbei wird in der Regel eine kontinuierliche Abtastrate verwendet.
Beispiel:
Bei Verwendung eines Kodierrades, aus dem 8 Sinusperioden gewonnen werden, entspricht dies einer Auflösung von 3 Bit. Wird dieses Sinussignal jedoch mit 10 Bit abgetastet, so ergibt sich eine (Digitalisier-)Auflösung von 213 Bit, was einer Auflösung von 8192 Imp./Udr. entspricht. Der Vorteil des Prinzips liegt also auf der Hand.
Es sind auch optische und magnetische Drehgeber mit Analogausgang erhältlich, die sinus- und kosinusförmige Analogsignale liefern. Mit einem solchen Geber ist eine nachgeschaltete Interpolation möglich.
Ausgangsschnittstellen
Inkrementale Signale eignen sich aufgrund ihrer Eigenschaften (hoch-niedrig, ein-aus, Bool‘sche Logik) besonders für die Zusammenarbeit mit digitalen Schaltungen. Viele Serien von Inkrementalgebern bieten daher Schnittstellen an, die eine einfache Integration in solche Schaltungen ermöglichen:
- OC (Open Collector)
- Standard-Spannungsausgang bzw. TTL (Transistor-Transistor-Logik)
- PP (Push Pull)
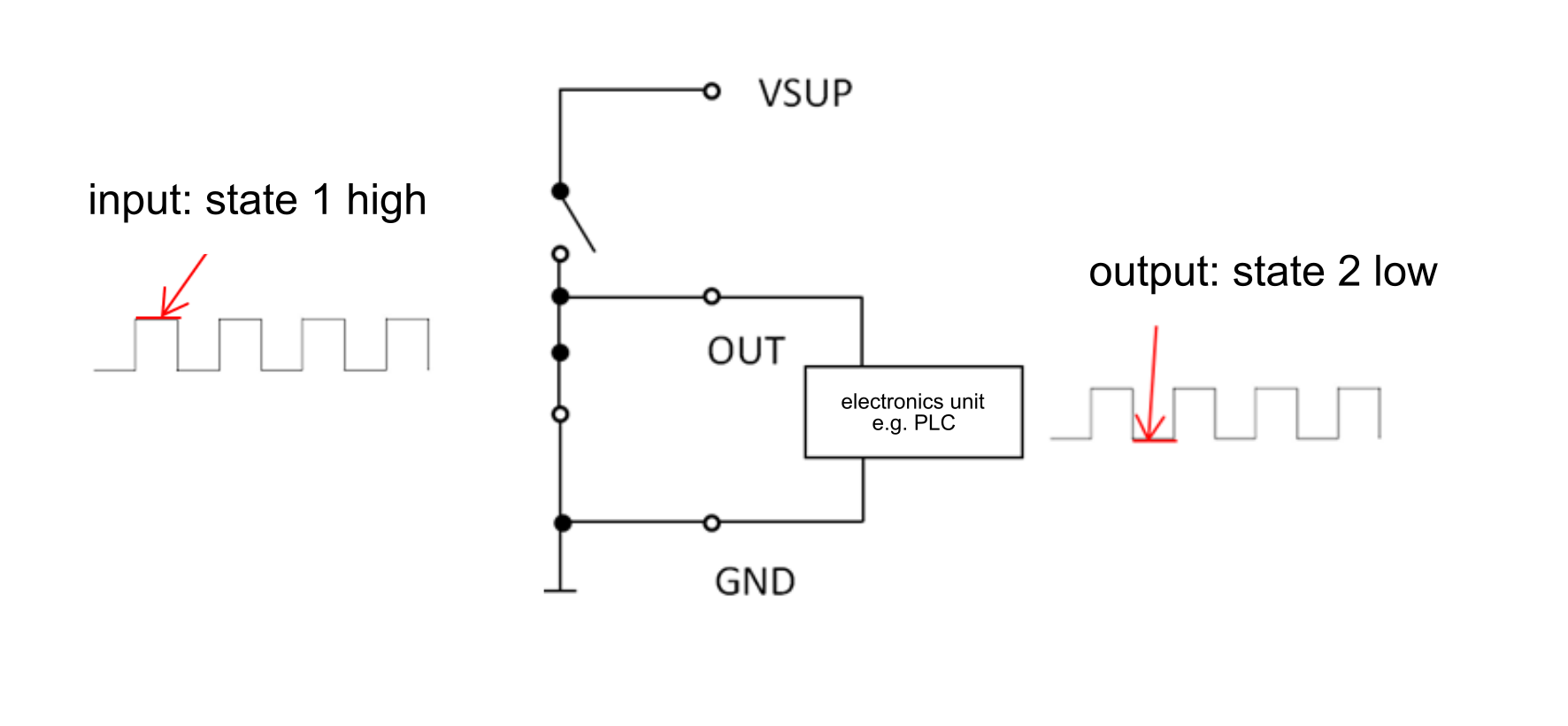
Open Collector (OC) Ausgang
Die Open-Collector-Schaltung ist ein offensichtlicher Standard für Ausgangsschaltungen für Inkrementalsignale. Sie bietet den großen Vorteil, dass der Ausgang an ein anderes, von der Anwendung definiertes Spannungsniveau angeschlossen werden kann. Dies ist möglich, da im Geber kein Pull-up-Widerstand integriert ist und der Kollektor ohne weitere Beschaltung aus dem Gehäuse herausgeführt ist (Open Collector). Der Transistor hat somit die Funktion eines Schalters.
Folgendes Beispiel ist für einen bipolaren Si-NPN Transistor anwendbar:
High Pegel am Signalausgang:
- Bei Low Pegel (<0,7 V) an der Basis des Transistors sperrt dieser und es liegt die Versorgungsspannung (VSUP) am Collector an.
Low Pegel am Signalausgang:
- Bei High Pegel (>0,7 V) an der Basis des Transistors wird die Spannung am Kollektor (VSUP) gegen Masse gezogen.

Bei der Open-Collector-Schaltung ist es in der Regel erforderlich, zwischen der Versorgungsspannung und den Signalausgängen A, B und Z des Gebers (Collector) jeweils einen Pull-Up-Widerstand zu platzieren. Damit wird sichergestellt, dass die Pegel von der Auswerteeinheit als Low- und High-Pegel erkannt werden können. Ein typischer Wert für den Pull-up-Widerstand kann 4,7 kOhm betragen. Die maximale Kollektorspannung hängt vom verwendeten Transistor ab und ist in der Regel im Datenblatt des Drehgebers angegeben. Da sie in einigen Fällen über 50 V liegt, können Inkrementalsignale mit sehr hohem Signalpegel über große Leitungslängen übertragen werden. Durch die Variabilität der Höhe der Kollektorspannung ist auch eine Pegelwandlung möglich.
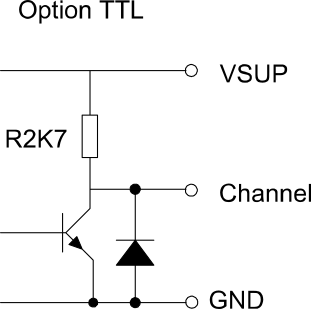
TTL-Ausgang
Der TTL-Ausgang wird oft auch einfach als Spannungsausgang (engl. voltage output) bezeichnet. Der Unterschied zum Open-Collector-Ausgang besteht darin, dass die erforderlichen Pull-Up-Widerstände bereits im Gebergehäuse integriert sind und damit die Pegel fest vorgegeben sind. Eine variable Pegelwandlung wie bei der Open-Collector-Schaltung ist daher nicht möglich.
Diese Pegel für Standard-TTL-Logik sind:
< 0,4 V für den Low-Pegel
> 2,4 V für den High-Pegel
Push / Pull Ausgang
Die Push/Pull-Ausgangsschaltung basiert auf einem komplementären Transistorpaar (n-Kanal und p-Kanal). Sie sperrt abwechselnd einen der beiden Transistoren.
Während des High-Pegels des Ausgangssignals liegt das Ausgangssignal an VSUP, während des Low-Pegels liegt das Ausgangssignal nahe an Masse. Der Vorteil einer Push/Pull-Schaltung besteht darin, dass keine zusätzlichen Pull-up- oder Pull-down-Widerstände erforderlich sind. Wenn keine Pegelwandlung erforderlich ist, können Drehgeber mit Push/Pull-Ausgangsschaltung als universeller Ersatz für Open-Collector- und TTL-/Spannungsausgänge verwendet werden.
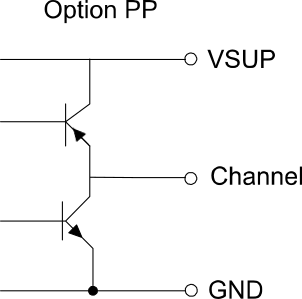
Low-Pegel an den Transistoreingängen: NPN sperrt und PNP öffnet
High-Pegel ist VSUP
Pegel High an den Transistoreingängen: NPN öffnet und PNP sperrt
Pegel Low annähernd auf Masse
Inkrementalgeber werden überall dort eingesetzt, wo Winkel, Drehzahlen oder Winkelgeschwindigkeiten mit hoher Genauigkeit erfasst werden müssen. Dabei liefern Inkrementalgeber Ausgangssignale in Form von Impulsen, die von einer externen Auswerteeinheit gezählt werden. Die Sensorik selbst basiert bei den hochwertigen Produkten von MEGATRON auf berührungslosen Messprinzipien wie optoelektronischer und magnetischer (Halleffekt) Sensorik.
Grundsätzlich kann festgehalten werden, dass optische inkrementale Drehgeber unempfindlich gegenüber externen Störfeldern sind und die höchste Genauigkeit bei Positionier- oder Verstellvorgängen bieten. Magnetische Drehgeber sind extrem langlebig und sehr robust gegenüber Vibrationen. Durch die große Vielfalt an Bauformen und Ausgangsoptionen findet sich in unserem Portfolio für nahezu jede Anwendung ein optimal geeigneter Inkrementalgeber.
Für spezielle Anwendungen sind jedoch oft technische Anpassungen erforderlich, die wir bei MEGATRON bereits bei relativ kleinen Stückzahlen realisieren. Unser Anspruch ist es, jedem Kunden individuell das funktionell und wirtschaftlich beste Produkt für seine Anwendung anzubieten. Von der Anfrage über die Serienreife bis zum Ende des Produktlebenszyklus unterstützen wir Sie als zuverlässiger Partner mit hoher Liefertreue und Qualitätssicherung.
 EN
EN DE
DE ES
ES FR
FR IT
IT